Home Teaching Publications Service Software Open Access Media Bio WebLog Opinions Contact

An historical survey of results

There has been a very interesting work dedicated to the characterization of the isomorphisms holding in some special classes of categories  [Sol83], even since 1981. 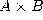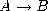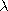In his work,   Soloviev focuses on a special class of categories, called cartesian closed categories, where for any two   objects AA and BB there exists a product , an exponent , and a special   object T called the terminal object,  with a set of additional properties that make them very well suited as   models of the typed -calculus (see for example [Sza78, LS86] and Chapter 8 of [AL91]).

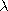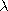If categorical tools are increasingly used to give semantics to programming languages, especially to functional ones, this is also due to a close connection between this class of categories and the typed -calculus. It is by now a very well known fact that the   models of -calculus with products and unit type are exactly the cartesian closed categories (shortly, ccc's), or, equivalently, that this calculus is the internal language of ccc's (see [Min77, LS86, AL91]). 

Due to this connection, this categorical problem coincides with the characterization of isomorphisms in typed lambda calculus, which is particularly interesting for the case of ccc's. It is a simple exercise in basic category   theory to show that in any ccc, the following isomorphisms hold:

 

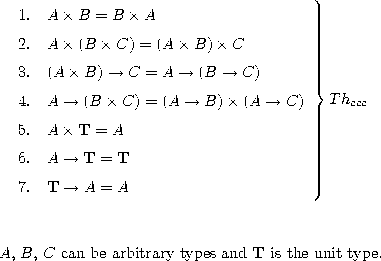
Table 1: The   theories of valid isomorphisms for   ccc's. 

In 1981,   Soloviev showed, using techniques developed in number   theory several years before, that these are exactly the isomorphisms holding in all ccc's. It is worthwhile to present here in some more details the connection with number   theory used by Soloviev, as it is another interesting case of connection  between very different branches of Mathematics.

If we take the table of isomorphisms of types above and we read it by taking T as the number 1, type variables as numerical variables, AABB 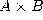as the regular product AB of two numerical expressions A and B, and finally AABB 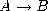as the   exponent 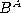, then the isomorphisms above become very well-known numerical identities that are taught in high-school algebra classes. The reason for this is that natural numbers can be used to build a cartesian closed category: to each n we associate a finite set with n elements, and as morphisms between two   objects m and n we take the 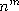usual set theoretic functions between the associated finite sets. In this category, the terminal object  is the singleton associated with 1, while the product and   exponent correspond directly to numerical product and exponentiation. Using these facts, it is easy to show that two   objects are isomorphic in the category of finite sets if and only if they are equal as numerical expressions. This means that we have reduced the problem of characterizing isomorphic types in the category of finite sets to the problem of finding all valid numerical   equation between expressions built out of product,   exponentiation and the constant 1 only. This number theoretic problem is a particular case of what is known under the name of   Tarski's High School   Algebra Problem, and has as a solution exactly the set of   equations of the Table 1 above. This remarkable fact allows us to conclude Soloviev's argument as follows: on one side, we have a set of isomorphisms that is valid in all   ccc's; on the other hand, we have found a special   ccc where only these isomorphisms hold. Hence, there cannot be any other isomorphism holding in all   ccc's, and we are done.

• Digression: Tarski's High School Algebra Problem
• Other classes of categories

Based on a CSS designed by James Koster via OSWD.