Home Teaching Publications Service Software Open Access Media Bio WebLog Opinions Contact

 

Digression:   Tarski's High School Algebra Problem

It would be unfair here not to give at least a brief description of the works in  number   theory that made possible this first elegant characterization of the isomorphisms that hold in all   ccc's. We will give here a general overview of the works in this field known to the author, as well as a list of references for the interested reader. In [DT69],   Tarski first asked if the following   usual equalities (called   theory 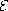) that are taught in high school are complete for the natural numbers (i.e., if they are enough to prove all the true numerical equalities):

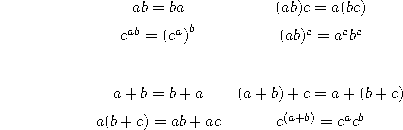
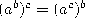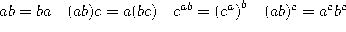He conjectured that they were enough, but was not able to prove his conjecture. His student   Martin could show that is complete for ,  and also that are complete for 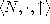,   but he exhibited a simple valid equation involving   sums that is not provable from these axioms:

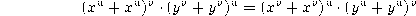
The question, though, was not settled by this counterexample, because it is a counterexample only if we do not allow a constant for 1, that   Tarski clearly considered necessary, even if he did not explicitly mention it in his conjecture. In the presence of a constant 1, the following new   equations come into play, and allow us to easily prove   Martin's equality. 

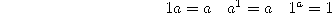
This problem attracted the interest of many other mathematicians, like Leon Henkin, who focused on the equalities valid in 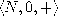, and showed the   completeness of the usual known axioms (commutativity, associativity of the sum and the zero axiom), and gives a very nice presentation of the topic in [Hen77]. 

Wilkie was the first to show with a proof theoretic approach in [Wil81] that even with 1 and the new axioms that come with 1, there are true identities that are not provable, like   

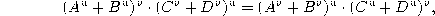
where A=(x+1), , , .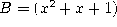

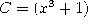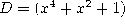Gurevic later gave a simpler   model theoretic proof of this fact [Gur85] and showed finally that for the valid equalities of 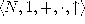there is no finite axiomatization  , by means of an indexed family of equalities that generalize Wilkie's identity [Gur90]. Nonetheless, equality in all these structures, even if not finitely axiomatizable, is decidable [Mac81, Gur85].

As often happens in number theory, these last results use far more complex tools than simple arithmetic reasoning, as in the case of  [HR84], where Nevanlinna   theory is used to identify a subclass of numerical expressions for which the usual axioms for +, , 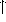and 1 are complete.

This remarkable analogy between isomorphisms and equalities in number theory works quite well for the first-order case, even if it seems quite hard to find an extension to higher-order languages.

Based on a CSS designed by James Koster via OSWD.